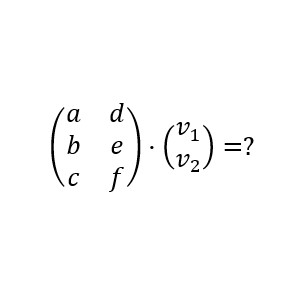Linear transformation of matrices are linear operations using matrices that modify the initial dimension of a given vector.

In other words, we can modify the dimension of a vector by multiplying it by any matrix.    

Linear transformations are the basis of the vectors and eigenvalues ​​of a matrix since they depend linearly on each other. 

Recommended articles: operations with matrices , vectors and eigenvalues . 

Mathematically

We define any matrix  C of dimension 3 × 2 multiplied by a vector V of dimension  n = 2 such that V = (v ₁ , v ₂ ). 

What dimension will the result vector be?

The vector resulting from the product of the matrix  C _{3 × 2} with the vector  V _{2 × 1} will be a new vector V ‘of dimension 3.  

This change in dimension of the vector is due to the linear transformation by the matrix  C .

Practical example 

Given the square matrix  R with dimension 2 × 2 and the vector  V of dimension 2.

A linear transformation of the dimension of vector  V is: 

where the initial dimension of vector  V was 2 × 1 and now the final dimension of vector  V is 3 × 1. This change in dimension is achieved by matrix multiplication  R .

Can these linear transformations be represented graphically? Well of course!

We will represent the result vector V ‘on a plane. 

So:

V = (2.1) 

V ‘= (6.4)

Graphically

Eigenvectors by graphical representation

How can we determine that a vector is an eigenvector of a given matrix just by looking at the graph?

We define the 2 × 2 dimension matrix  D : 

Are the vectors v ₁ = (1,0) and v ₂ = (2,4) eigenvectors of the matrix D ?

Process

1. Let’s start with the first vector v ₁ . We do the above linear transformation: 

So if vector v ₁ is actually eigenvector of matrix D , the resulting vector v ₁ ‘and vector v ₁ should belong to the same line.

We represent v ₁  = (1,0) and v ₁ ‘= (3,0). 

Since both v ₁ and v ₁ ‘belong to the same line, v ₁ is an eigenvector of the matrix  D .

Mathematically, there is a constant  h (eigenvalue) such that: 

2. We continue with the second vector v ₂ . We repeat the above linear transformation: 

So, if vector v ₂ is really eigenvector of matrix D , the resulting vector v ₂ ‘and vector v ₂ should belong to the same line (like the previous graph). 

We represent v ₂  = (2,4) and v ₂ ‘= (2,24). 

Since v ₂ v ₂ ‘non Similarly, v ₂ is an eigenvector of the matrix  D . 

Mathematically, there is no constant  h (eigenvalue) such that: 

<!–

–>